Ley de ohm

La ley de Ohm dice que la intensidad que circula entre dos puntos de un circuito eléctricoes proporcional a la tensión eléctrica entre dichos puntos. Esta constante es la conductancia eléctrica, que es lo contrario a la resistencia eléctrica.

La intensidad de corriente que circula por un circuito dado, es directamente proporcional a la tensión aplicada e inversamente proporcional a la resistencia del mismo.

Georg Ohm

La ecuación matemática que describe esta relación es:



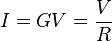
Donde, I es la corriente que pasa a través del objeto en amperios, V es la diferencia de potencial de las terminales del objeto en voltios, G es la conductancia en siemens y R es la resistencia en ohmios (Ω). Específicamente, la ley de Ohm dice que R en esta relación es constante, independientemente de la corriente.1

Esta ley tiene el nombre del físico alemán Georg Ohm, que en un tratado publicado en 1827, halló valores de tensión y corriente que pasaba a través de unos circuitos eléctricos simples que contenían una gran cantidad de cables. Él presentó una ecuación un poco más compleja que la mencionada anteriormente para explicar sus resultados experimentales. La ecuación de arriba es la forma moderna de la ley de Ohm.

Esta ley se cumple para circuitos y tramos de circuitos pasivos que, o bien no tienen cargas inductivas ni capacitivas(únicamente tiene cargas resistivas), o bien han alcanzado un régimen permanente (véase también «Circuito RLC» y «Régimen transitorio (electrónica)»). También debe tenerse en cuenta que el valor de la resistencia de un conductor puede ser influido por la temperatura.

Circuitos en Resistencia

Descubierta por Georg Ohm en 1827, la resistencia eléctrica tiene un parecido conceptual a la fricción en la física mecánica. La unidad de la resistencia en el Sistema Internacional de Unidades es el ohmio (Ω). Para su medición en la práctica existen diversos métodos, entre los que se encuentra el uso de un ohmímetro. Además, su cantidad recíproca es la conductancia, medida en Siemens.

La resistencia de cualquier objeto depende de su geometría y de su coeficiente de resistividad a determinada temperatura: aumenta conforme es mayor su longitud y disminuye conforme aumenta su grosor o sección transversal.

Además, de acuerdo con la ley de Ohm la resistencia de un material puede definirse como la razón entre la caída de tensión y la corriente en dicha resistencia, así:

Donde R es la resistencia en ohmios, V es la diferencia de potencial en voltios e I es la intensidad de corriente enamperios.

Comportamientos ideales y reales

Una resistencia ideal es un elemento pasivo que disipa energía en forma de calor según la ley de Joule]]. También establece una relación de proporcionalidad entre la intensidad de corriente que la atraviesa y la tensión medible entre sus extremos, relación conocida comoley de Ohm:

donde i(t) es la corriente eléctrica que atraviesa la resistencia de valor R y u(t) es ladiferencia de potencial que se origina. En general, una resistencia real podrá tener diferente comportamiento en función del tipo de corriente que circule por ella.

Comportamiento en corriente continua

Una resistencia real en corriente continua (CC) se comporta prácticamente de la misma forma que si fuera ideal, esto es, transformando la energía eléctrica en calor por efecto Joule. La ley de Ohm para corriente continua establece que:

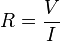
donde R es la resistencia en ohmios, V es la diferencia de potencial en voltios e I es la intensidad de corriente enamperios.

Asociación de resistencias

Resistencia equivalente

Se denomina resistencia equivalente de una asociación respecto de dos puntos A y B, a aquella que conectada la misma diferencia de potencial,UAB, demanda la misma intensidad, I (ver figura 4). Esto significa que ante las mismas condiciones, la asociación y su resistencia equivalente disipan la misma potencia.

 Asociaciones generales de resistencias: a) Serie y b) Paralelo. c) Resistencia equivalente.

Asociación en serie

Dos o más resistencias se encuentran conectadas en serie cuando al aplicar al conjunto una diferencia de potencial, todas ellas son recorridas por la misma corriente.

Para determinar la resistencia equivalente de una asociación serie imaginaremos que ambas, figuras 4a) y 4c), están conectadas a la misma diferencia de potencial, UAB. Si aplicamos la segunda ley de Kirchhoff a la asociación en serie tendremos:

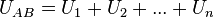
Aplicando la ley de Ohm:

En la resistencia equivalente: 

Finalmente, igualando ambas ecuaciones se obtiene que:

Por lo tanto, la resistencia equivalente a (n) resistencias montadas en serie es igual a la sumatoria de dichas resistencias.

Asociación en paralelo

Dos o más resistencias se encuentran en paralelo cuando tienen dos terminales comunes de modo que al aplicar al conjunto una diferencia de potencial, UAB, todas las resistencias tienen la misma caída de tensión, UAB.

Para determinar la resistencia equivalente de una asociación en paralelo imaginaremos que ambas, figuras 4b) y 4c), están conectadas a la misma diferencia de potencial mencionada, UAB, lo que originará una misma demanda de corriente eléctrica, I. Esta corriente se repartirá en la asociación por cada una de sus resistencias de acuerdo con la primera ley de Kirchhoff:

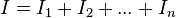
Aplicando la ley de Ohm:

En la resistencia equivalente se cumple: 

Igualando ambas ecuaciones y eliminando la tensión UAB:

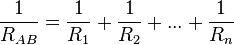
Asociación mixta

 Asociaciones mixtas de cuatro resistencias: a) Serie de paralelos, b) Paralelo de series y c) Ejemplo de una de las otras posibles conexiones.

En una asociación mixta podemos encontrarnos conjuntos de resistencias en serie con conjuntos de resistencias en paralelo. En la figura 5 pueden observarse tres ejemplos de asociaciones mixtas con cuatro resistencias.

A veces una asociación mixta es necesaria ponerla en modo texto. Para ello se utilizan los símbolos "+" y "//" para designar las asociaciones serie y paralelo respectivamente. Así con (R1 + R2) se indica que R1 y R2 están en serie mientras que con (R1//R2) que están en paralelo. De acuerdo con ello, las asociaciones de la figura 5 se pondrían del siguiente modo:

a) (R1//R2)+(R3//R4)

b) (R1+R3)//(R2+R4)

c) ((R1+R2)//R3)+R4

Para determinar la resistencia equivalente de una asociación mixta se van simplificando las resistencias que están en serie y las que están en paralelo de modo que el conjunto vaya resultando cada vez más sencillo, hasta terminar con un conjunto en serie o en paralelo. Como ejemplo se determinarán las resistencias equivalentes de cada una de las asociaciones :

a)   R1//R2 = R_1//2

R3//R4 = R_3//4

R_AB = R_1//2 + R_3//4

b)  R1+R3 = R₁₊₃

R2+R4 = R₂₊₄

R_AB = R₁₊₃//R₂₊₄

c)   R1+R2 = R₁₊₂

R₁₊₂//R3 = R_1+2//3

R_AB = R_1+2//3 + R4

Desarrollando se obtiene:

a)

b)

c)

Ejercicios Resueltos